Final update

Toni decided to respond to this post with his on-brand oblivious aggressiveness. As you can see in the comments, the “discussion” quickly devolved to open threats, culminating in an explicit threat from the official Hoosat network account. In this post he also presented me as the “Kaspa head of research” despite no such position even existing (and if it were, it would be Yonatan’s position), which I guess is a nice upgrade from “the inventor of kHH” as far as fake titles go, he pretty much ignored everyone’s proclamations that this is stupid. Throughout the communication he kept hinting that if I publicly apologize he will not post his attack, which is textbook extortion.

I tried to explain that publicly disclosing a vulnerability is a breach of ethics that’ll follow him throughout his career, and nobody would particularly care how pissed off he was at the time, how “unethical” he thinks the other side was, or whether the vulnerability actually works.

He stopped responding, so I thought he got the message and this is behind us. But he decided to follow through with his unethical conduct, making a post with the very humble and non-confrontational title How to attack Kaspa! (that he obviously also promoted on the official Hoosat account). Now I warn the reader in advance that this post is rather… unhinged. It starts with five paragraphs of excusing his conduct because I was mean to him in my comments (which I was, which you could argue was unwarranted [which I disagree with] or impolite [which I agree with], but there was nothing unethical about it).

In his post he claims that a small miner can improve his revenue eight times using his strategy (that has been christened with the name 0×51 mining).

This is obviously military grade nonsense, as I explained it detail. I did make one small mistake there though: It is not true that Toni attacks the pre_pow_hash. I thought he did because he keep talking about “per block” attacks, where the real attack is “per nonce”, I still don’t understand why he’s talking in terms of “per block”, but at this point I think there is no deep reason and that’s just a symptom of constantly word-salading your way through a discussion that’s supposed to be technical.

Toni responded with his on-brand hissy fit, pontificating on small irrelevant details (and getting them wrong) and completely ignoring the essentials. At this point it was abundantly clear that this guy would do and say anything to have the last word, so I decided to put my money where my mouth is, and offered him a bounty of up to $50k in donations to Hoosat development if he actually codes a miner that successfully applies this attack (which could be easily tested on our testnet).

His response was “Seriously go to hell with your money,” along with a threat that to “upload GPU Kaspa OpenCL miner today to hunt for 0x51.” Which only seven minutes later, he did. Supposedly. Looking at the commit history to his fork of the miner code, we only find one relevant commit, that does the following change:

That is, he just removed the entire matMult step and just assumed that it always returns the same result. No “timed attacks”, no “guessing which blocks will have a 0×51 product value”, just plain brute-force. I assume I don’t have to explain again why this is completely broken.

For me, this concludes the discussion. Toni proved that he has neither professional ethics no professional acumen. The way I see it, a person that is willing to sacrifice his ethics for vindictiveness will also sacrifice it for greed. If he betrayed the trust of his peers he could just as easily betray the trust of his colleagues and community. In his own words: “I know who I am. I’m dangerous person.”

Toni also proved that he will do absolutely everything to say the last word, so he can have it with my blessing. I will not respond to any follow-ups on this alleged attack before I see a working miner that demonstratably provides a non-negligible improvement (though as I explained before, even if such a miner does emerge, it is inconsequential. But I still argue that it is impossible out of principle).

Final update deluxe: Hoohash is nonsense

End of update

Recently, Toni Lukkaroinen (founder of something called Hoosat Network) posted two articles (original and follow-up) where he alleges the kHeavyHash is “broken”.

These allegations are obviously very far from the truth, and explaining exactly why is a great opportunity for an instructive discussion about hashes, HeavyHash, and professional ethics. For those who just want an executive summary, the next section should provide all you need. The rest are invited to a deep dive that will surely benefit your understanding of the inner-workings of proof-of-work.

The tl;dr

The main points that are as follows:

• Toni points to some research of kHH carried out by Lolliedieb (the developer of lolMiner). In this research, Lolliedieb noticed that one of the computational steps in kHH called matMult provides less randomness than it was supposed to.

• This is a consequence of a bug in the implementation of matMult, while kHeavyHash was the subject, it actually applies just as well to the original HeavyHash algorithm. This was already noted in a public discussion almost three years ago, where it was determined this is a non-issue.

• Toni has been trying to argue that this implies a meaningful vulnerability in kHH that could affect the security of the network (though he later backtracked from that statement). However, as Lolliebeck interjected himself, the most severe possible consequences are that there might be mining strategies that could skip the matMult stage. He also agrees that calling kHH broken based on this is unreasonable, and points out that his work and name were used without his permission.

• I will discuss matMult below, but for now it suffices to point out that this step constitutes about 10% of the computational steps when computing kHH on a GPU, and about 20% on ASICs. That is, even if a strategy is found to skip this step without any overhead, that would still only incur a small improvement. In reality, such a strategy will have overhead which will make it even less meaningful as an optimization, and plausibly greater than the gain. Lolliebeck thinks it is “likely” that eventually ASICs will be designed to skip this step, I think it is not that obvious, but either way this is just another increment in ASIC optimization. Current ASICs are already more than ten times or more more efficient than the first generation of ASICs (in terms of hashes per Watt), a few more percent of optimization is not going to make or break anything.

• The significance of matMult was that it was believed this particular step would be very easy and cheap to compute on optical chips, ushering in optical mining. However, later research revealed that this matrix is not suitable for optical mining so any project going the optical route could not use the current implementation of HeavyHash anyway. A new OPoW-appropriate implementation could fix this bug along the way.

• During the altercation, Lukkaroinen failed professional ethics at least thrice. First, by misrepresenting Lolliedieb’s work without consent. More importantly, by publicly disclosing an alleged vulnerability without privately disclosing it first. In the cryptography world, it is a very important practice to allow platforms that could be affected by an exploit some time to prepare precautions before making the vulnerability public. Surely, the vulnerability should be eventually made public, but only after measures were deployed to protect users from its consequences. In this case no harm was done, as the “vulnerability” is fake, but circumventing this important practice is deplorable either way. The third ethical failure was Lukkaroinen’s choice to have my comments on his original post removed.

Hash Functions

A hash function is an algorithm that is given an arbitrary input, and provides an output of some constant length. The security of a hash function is tricky to define. It is common to informally describe the security as follows: if I input any two different strings, then the output should look completely different. Even if the input is changed by a single bit, the output should appear completely random. As we will soon see, this requirement is actually too stringent, and the commonly used SHA-256 hash actually fails to achieve it (as I explain below excruciating detail). This means that there are situations where using SHA-256 is not secure. However, proof-of-work is not one of them. The reason I am pointing this out is to drive a point home: just because a hash function is not perfect, does not mean it is insecure to use it correctly. For a deeper discussion of what hash functions are, and how they are used in mining, see my book.

What Makes a Hash “Broken”

As I said, there are many ways to define the security of a hash function. I will informally describe four of them. All definitions follow the same template: I will describe some challenge $X$, and define that the hash is $X$-secure if it is “hard” to succeed in this challenge.

What makes my description informal is that we never defined what it actually means to be “hard”. A proper definition is too subtle for the current discussion, but to make it a little less vague (but still not completely formal) note that most of these tasks could be accomplished by brute-force: just try more and more inputs until you happen to land on the one that gets the job done. Hardness means that any strategy will require a good amount of brute-force.

Four challenges that are very common in the literature are:

• Preimage: given an output $y$, find $x$ such that $H(x)=y$.

• Collision: find $x_1\ne x_2$ such that $H(x_1) = H(x_2)$.

• Extension: given $H(x_1)$ for some secret $x_1$, find $x_2$ and $y$ such that $H(x_1\|x_2)=y$ (here $x_1\| x_2$ means string concatenation).

• Distinguishing: you are given access to a black box which is either the hash function $H$ or a truly random function $R$ (that is, you are allowed to feed it inputs and get outputs, but you can’t look inside the box), and you need to tell which is which.

So if it is hard to complete say the preimage task, we say that $H$ is preimage secure. Note that if $H$ is not preimage secure, then it is a very bad hash function. For example, it would make it very easy to find nonces, completely undermining proof of work. Collision security is more commonly called collision resistence, and is often considered the line in the sand that defines the validity of a hash function. While it is not straightforward how a collision attack could be translated into a more meaningful attack, it does provide indications of weakness and is usually considered a deal breaker. Historically, any hash that exhibited cheap collision attacks was ultimately broken in much more meaningful ways.

Extension is a very particular property, that I only brought up so I could say that SHA-256 is not extension-secure, and people still use it. Moreover, as we will see, this “weakness” in SHA-256 was known since its inception, and follows quite immediately from its design. This is a major example of a deliberate choice to use a hash function even though it is known to be less-than-perfect, which I explain below in excruciating detail.

Finally, if $H$ is distinguishing-secure we usually just call it indistinguishable. This is the strongest form of security that we could require from a hash function, and in many cases it is unrealistic. Despite common knowledge, hash functions could be perfectly fine to use in many situations even if there are known algorithms for distinguishing them from truly random outputs.

There could be many motivations to use hash functions even if they are known not to be perfect: it could be that they are more efficient, that they have gone through much more public scrutiny (so it might as well be the case that the “perfect” hash function is actually considerably more broken, we just don’t know it yet), and because the technical cost of redeploying the hash function might be way above any gains from doing so. The latter is the main reason replacing kHH is not seriously considered by anyone: the “gain” would be to prohibit a hypothetical marginal optimization that anyone can leverage (so it does not compromise fair mining), while the cost would be a hard-fork that renders all existing ASICs and mining software useless.

One useful observation about defining notions of security through the hardness of tasks is that it gives as a nice way to reduce one security notion to another: the harder the task is, the weaker the resulting security notion is. It is much easier to hack a safe if you are not a paraplegic, so it is much easier to design a safe secure against paraplegic burglars. More generally, if the ability to solve challenge X implies the ability to solve challenge Y, then being Y-secure is stronger than being X-secure. Let us apply this observation to the definitions above.

Say that I know how to preimage attack $H$: given any $y$, I can find $x$ such that $H(x)=y$. I can use this ability to find a collision: I’ll choose a random $x_1$, compute $y=(x_1)$ and use my preimage attack to find $x_2$ such that $H(x_2) = y = H(x_1)$. The only concern I have is that it might just happen that $x_1 = x_2$. However, by slightly tweaking the attack we can make sure that the probability this happens is very small. If we repeat the attack, resampling $x_1$ in each attempt, we will find $x_2 \ne x_1$ very soon. This proves that preimage security is weaker than collision security.

It might be a bit less clear, but I reckon most of you agree that if $H$ was completely random, and had no internal structure, than none of these attack would work. Hence, each such attack can used to distinguish $H$ from a truly random function. If my strategy for finding, say, a collision actually worked, then there is no way a truly random function hides in the box. Hence, a very large class of attacks are allows us to solve the distinguishing challenge, making indistinguishability a very strong notion of security.

Exercise: we’ve seen that preimage security is weaker than collision resistance which is weaker than indistinguishability. How does extension security fit into this hierarchy?

Extension attack on Merkle–Damgård hashes*

This part of the post is a digression from the actual discussion and can be completely skipped. I included it here because I think it provides a nice vantage into the world of cryptography that many readers would enjoy. However, it is a bit more technical than the rest of this post.

SHA-256 is a special case of something called the Merkle–Damgård construction (MD). Merkle and Damgård are bigshots, Merkle is the guy behind Merkle trees, and if you’ve ever heard of digests like MD5, now you know what the MD stands for.

The MD transforms does the following: it takes a collision resistant function $f$ with fixed input length and transforms it into a collision resistant hash called $MD_f$. The difference is that the latter can accept input of any length.

We note that the notion of collision only makes sense in cases where the domain is larger than the range. Otherwise, any injective function (such as $f(x)=x$) is trivially collision resistant. The MD transform is concerned with cases where the domain is exponentially larger than the range. In particular, we consider a circuit $f$ that takes $2d$ buts of input and outputs $d$ bits (so the domain is $2^d$ times larger than the range). Say you have designed such a circuit, and you are thoroughly convinced it is “hard” to find $x_1\ne x_2$ with $f(x_1) = f(x_2)$ (that is, there is no strategy to do so that requires much less than $2^d$ computational steps).

The MD construction allows you to transform $f$ into a function $MD_f$ that takes input of any length and produces $d$ bits. This construction has the following property: if you can find $x_1\ne x_2$ such that $MD_f(x_1) = MD_f(x_2)$, you could use them to find $x’_1 \ne x’_2$ such that $f(x’_1) = f(x’_2)$. That is, the MD construction preserves the difficulty of finding a collision.

I will describe the MD transform for the simple case where the inputs are always of a length which is a multiple of $d$. That is, I will only consider inputs of the form $x^{(1)}\|x^{(2)}\|\ldots\|x^{(k)}$ where each block $x_{(i)}$ is of length $d$. Note that the input of the function $f$ is two blocks.

The MD transform applied to the input $x = x^{(1)}\|x^{(2)}\|\ldots\|x^{(k)}$ is described by the following diagram:

The only “new” thing here is the string $IV$. This string is called the initialization vector and it is just an arbitrary binary string of length $d$. It is not secret, or random or anything, just a string we all agree upon (in fact, the only difference between HeavyHash and kHeavyHash is choosing a different $IV$).

Remark: It is tempting to generalize the construction to any length by “padding with zeros”. That is, if the input is of size $\ell$ with $\ell \not\equiv 0 \mod d$, we just append $d - (\ell \% d)$ zeros to complete the last block. This is in fact completely broken. Exercise: find a very simple collision attack on the resulting hash. Obviously there are correct ways to generalize MD to arbitrary lengths, but they are very subtle. This is just one more example of how hard cryptography is, and how even seemingly benign decisions can have catastrophic consequences if they are not thought out properly.

Proving that a collision in $MD_f$ implies a collision in $f$ is straightforward. I will only prove it for inputs of length $2d$ and leave the general case to the reader (note that the general case includes inputs of different lengths, and in particular the case where one input is a prefix of the other input). The proof might seem a bit tedious, but there is nothing deep to it, only a bit of careful bookkeeping.

Assume $x_1 = x_1^{(1)} \| x_1^{(2)}$ and $x_2 = x_2^{(1)} \| x_2^{(2)}$ satisfy that $x_1 \ne x_2$ yet $MD_f(x_1) = MD_f(x_2)$ (or equivalently, $y^{(2)}_1 = y^{(2)}_2$). We consider two cases:

• If $x_1^{(1)} \ne x_2^{(1)}$ then one of the following happens:

  • $y_1^{(1)} = y_1^{(2)}$, that is $f(IV \| x_1^{(1)}) = f(IV\|x_1^{(2)})$ despite $IV \| x_1^{(1)} \ne IV \| x_1^{(2)}$, so we found a collision in $f$.

  • Otherwise, $y_1^{(1)} \ne y_1^{(2)}$ implies that $y_1^{(1)}\|x_1^{(2)} \ne y_1^{(2)}\|x_2^{(2)}$ and yet $f(y_1^{(1)}\|x_1^{(2)}) = y_1^{{(2})} = y^{(2)}_2 = f(y_1^{(2)}\|x_1^{(2)})$, which is again a collision in $f$.

• If $x_1^{(1)} = x_2^{(1)}$ then we must have $y_1^{(1)} = y_1^{(2)}$ yet now it is promised that $x_1^{(2)} \ne x_2^{(2)}$ (otherwise we would have had that $x_1=x_2$) so a contradiction follows the same way as the second case above.

The next thing to note is that there is a length extension attack on $MD_f$ (regardless what $f$ is), and this is actually quite simple. Say that $x = x^{(1)}\|\ldots\|x^{(k)}$ and we are given $MD_f(x)$ but not $x$. Let $z$ be any string of length $d$. Then one can easily see that $MD_f(x\|z) = f(MD_f(x)\|z)$, which we could calculate without knowing $x$ at all!

To see why this could be a problem, let us consider message authentication codes (MAC). In a MAC scheme, Alice and Bob create a private-key $pk$ together. Alice can then create a message $m$ and send it to Bob along with a MAC tag $t_m$. The security of a MAC scheme implies that Bob could use $pk$ and $t_m$ to validate the authenticity of $m$. That is: there is some way for Bob to assure that $t_m$ was indeed created by Alice from the message $m$. Given a hash function $H$, we can consider the following MAC scheme: $pk$ is just a random string. When Alice creates the message $m$, she also creates the tag $t_m = H(pk\|m)$. When Bob gets the message $m$ and the tag $t_m$ he verifies that indeed $t_m = H(pk\|m)$.

One can prove that if $H$ is a perfect hash function then the scheme above is perfectly secure. However, if it is not extension secure (for example, if it is an MD transform) then it can be compromised: say Alice sends to Bob the string $x=$”pay Charlie €1,000”, then Charlie could choose $z=$”,000” and by applying a length extension attack compute $t_{m\|z}$. The result is that Bob will receive the message $x\|z=$”pay Charlie €1,000,000” along with a completely valid MAC tag and would be none the wiser.

It should be noted that this example never happened in practice. It was manufactured as a textbook example. Moreover, the scheme above is easily fixable to remain secure even when instantiated with $MD_f$. Figuring out how will remain an exercise to the reader.

To conclude we will only point out that the SHA3 family of hashes (including Keccak) does away with the MD transform in favor of a more modern approach called the sponge construction. This approach was chosen for its ASIC friendliness, but it is also assumed to prohibit length extension attacks.

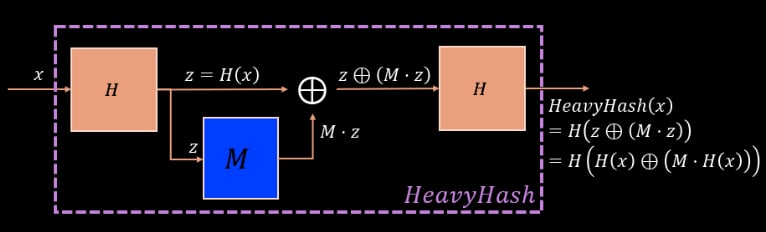
HeavyHash

In the abstract, HeavyHash is not a hash function by itself but a transformation. It allows us to choose a hash function $H$ and “sandwich” a matrix multiplication operation (often just called matMult) in between. This looks like this:

Let us go over some of the stuff that’s going on there.

HeavyHash is not Broken

The first thing I want to convince you is that any break in HeavyHash implies a similar break in Keccak. For that we need to understand the way matMult is embedded in HeavyHash.

The $\oplus$ sign indicates the exclusive OR (XOR) operation. The XOR operation is given two bits and outputs $1$ if they are different or $0$ if they are the same: $0\oplus 0 = 1\oplus 1 = 0$, and $0\oplus 1 = 1 \oplus 0 = 1$. When applied to a string of bits, XOR just works component wise, that is, $(x\oplus y)_i = x_i \oplus y_i$. So for example $(0110)\oplus(1100) = 1010$.

Another nice way to think about XOR is like lamps. Say you have $256$ lamps, some are lit and some are not. The string $x$ records, for each lamp, whether it is lit (1) or not. Now someone wants you to toggle some of the lamps — light them if they aren’t lit, turn them off if they are — so they send you a string $y$ that tells you what lamps should be toggled (1) and what should not (0). The string $x\oplus y$ records what lamps are lit after you followed the instructions.

There are two important facts about XOR:

1. XOR is injective: if $x_1\ne x_2$ then $x_1\oplus y \ne x_2 \oplus y$, no matter what $y$ is.

2. If the string $x$ is uniformly random, then the string $x\oplus y$ is also uniformly random, regardless of the string $y$. Even if the string $y$ is known, it tells you nothing about the string $x\oplus y$.

The second property implies that, due to the XOR operator, even if matMult is completely broken in the sense that there exists a perfect guesser that always knows the result for free, the security of HeavyHash is never compromised. Hence, calling HeavyHash broken is an egregious exaggaration. It provably enjoys the same security of the underlying hash.

For example, here is a sketch of the reduction for collision resistant: suppose you could easily find two strings $x_1,x_2$ such that $HH(x_1)=HH(x_2)$. That is $H(H(x_1)\oplus (M\cdot H(x_1))) = H(H(x_2)\oplus (M\cdot H(x_2)))$. If $H(x_1)\oplus (M\cdot H(x_1)) \ne H(x_2)\oplus (M\cdot H(x_2))$ then we have found a collision in $H$. Otherwise we have that $H(x_1)\oplus (M\cdot H(x_1)) = H(x_2)\oplus (M\cdot H(x_2))$. If we assume that matMult is very random, the probability for this is extremely small. If we assume that it isn’t, we will not have to repeat this many times before we find $x_1,x_2$ that additionally satisfy that $M\cdot H(x_1) = M\cdot H(x_2)$, so it follows that $H(x_1) = H(x_2)$ and again, we found a collision in $H$.

MatMult’s “weakness”

For reasons I will not get into, we denote the result of applying the matMult operation to a string $z$ as $M\cdot z$. There is no reason to explain what the matMult operation exactly does. All you need to know is this: it was supposed to be very random, that is, if $z$ is uniformly random, we expected that $M\cdot z$ is also uniformly random. However, due to an implementation error (which is as simple as using the number 10 where the number 6 should have been used), it is not. In fact, it is highly concentrated.

What does this mean? That there is a particular string $s$ such that if $z$ is random, then $M\cdot z = s$ is much more likely than other strings. How likely? It is hard to know, but according to empirical data the probability of landing on this string is $0.77^{64} \approx 0.0000054\%$ or about one in $18$ million (for some reason, Toni’s post does the exact same calculation but somehow gets that $0.77^{64} \approx 0.000334\%$ which is definitely not true, and more than 50 times larger than the actual value). For comparison, if matMult was working as advertised, the probability would have been one in $2^{256}$, which is much smaller.

So, how can this be used to circumvent the matrix multiplication stage? The idea is that instead of actually computing $M\cdot z$ we just guess that the result is $s$. We would be correct one in $18$ million times. So it will take us $18$ million attempts to find a nonce that actually hashes correctly, but we shaved off $10\%$ of each attempt.

This isn’t very good now is it? If we only spend $90\%$ of the time on each hash, but we need $18$ million times more hashes this still means that finding a hash this way will take $16.2$ million times more time.

The reason for that is that while this strategy is very simple, it is also very stupid. And we can try to improve it.

Toni suggests the following improvement: he isolates a family of $65$ different strings. One can compute that the probability that we fall within one of these strings is $0.77^{64} + 64\cdot 0.77^{63}\cdot 0.125 \approx 0.0006\%$ or about one in $160$ thousand. How will the attack go now?

For each nonce, we guess the product is one of these 65 values. We have to compute the first $H$ once and the second $H$ 65 times, which in total takes $30$ times more than computing a single hash, and we will only have to repeat this about $160,000$ times until success, which is only 5 million times more. This is still hardly good enough, but we see that with just a simple adjustment we are already four times better than we started.

The question that remains is: can we find a set of values that is small yet likely enough so that employing such a strategy will actually be more efficient than just doing the matrix multiplication step. This is a hard question for many reasons. First, the probability of $M\cdot z$ is complicated. Second, in my computation I ignored the fact that the larger the set is, the more complicated the circuit becomes, which might add even more overhead that makes this approach unfeasible. I remind you that the perfect guesser that is always correct and has no overhead could provide an improvement of at most 20%, how much of an optimization do you think a realistic guesser could provide, if any? Third, note that the attack requires sending many invalid blocks. Since the attacker can’t verify the correctness of their guess without computing matMult themselves. Hence, such an optimization would somehow have to deal with peers constantly blacklisting your nodes for spamming the network with invalid blocks.

So the bottom line is that we went from “HeavyHash is broken” all the way to “Someone told me about an implementation detail that might provide a very moderate optimization to computing HeavyHash, but despite attempts from both Lolliedieb and myself, we haven’t found a way to actually leverage this into a working optimization”.

And that’s about it. Questions?

Update: The probabilities computed above are based on a particular independence assumption. For reasons I will not go into, it is natural to interpret the string $M\cdot z$ not as $256$ bits but as $64$ strings of $4$ bits, that is, as a number between $0$ and $15$. In the simulations I appealed to, I realized that the probability that some coordinate is $3$ is $77\%$ and the probability that it is $2$ is $12.5\%$ (and all other values are significantly less likely). If we assume all coordinates are independent, this implies that the probability to get $64$ coordinates of value $3$ is $0.77^{64}$, and this is the string $s$ I was talking about. Similarly, in the second strategy I described the $65$ strings are the “all three“ strings, and the $64$ strings that have $63$ threes and one two. Assuming independence the probability to get a particular string of the second form is $0.77^{63}\cdot 0.12$, so the probability to get any of the strings in the set is $0.77^{64}+64\cdot 0.66^{63}\cdot 0.12$. Lukkaroinen claims that according to his measurements these strings appear more often. He claims that the all three strings appears about once every 10k blocks and the “all three except maybe one two” set appears about once every 1500 blocks. This seems dubious to me since this implies very strong correleation between the coordinates that result from multiplying a random matrix by a random vector, but whatever. Even if it is true, we still get that the first attack is 8000 times slower than standard mining, and the second is 32000 times slower (yes, in this case the second strategy is actually worse). It is easy to compute that for the “all threes” attack to actually provide any improvement (assuming 20% matMult) it has to appear more than four out of every five times. Even in its “highly concentrated” state, matMult provides enough randomness to make the optimization unreachable.